Home  ›  what average speed does he need to reach in his second round

what average speed does he need to reach in his second round

Written By Thursday, April 7, 2022 Add Comment Edit

Chapter viii: Rational Expressions

8.viii Charge per unit Give-and-take Problems: Speed, Distance and Time

Distance, rate and time bug are a standard application of linear equations. When solving these problems, use the relationship charge per unit (speed or velocity) times time equals altitude.

\[r\cdot t=d\]

For case, suppose a person were to travel thirty km/h for 4 h. To discover the total distance, multiply charge per unit times time or (30km/h)(4h) = 120 km.

The problems to be solved here volition accept a few more steps than described to a higher place. So to keep the information in the problem organized,  use a table. An case of the bones structure of the table is below:

Case of a Altitude, Rate and Time Nautical chart
Who or What Charge per unit Fourth dimension Distance

The third column, distance, will e'er be filled in by multiplying the charge per unit and time columns together. If given a full distance of both persons or trips,  put this information in the distance column. Now use this table to gear up and solve the post-obit examples.

Joey and Natasha start from the same point and walk in opposite directions. Joey walks ii km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?

Who or What Rate Fourth dimension Distance
Natasha r \text{3 h} \text{3 h}(r)
Joey r + 2 \text{3 h} \text{3 h}(r + 2)

The distance travelled by both is 30 km. Therefore, the equation to be solved is:

\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \\ \midrule &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&r&=&4 \text{ km/h} \end{array}

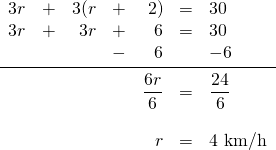
This ways that Natasha walks at 4 km/h and Joey walks at 6 km/h.

Nick and Chloe left their camp by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. Later on how much time did the campers plough around downstream?

Who or What Rate Fourth dimension Distance
Downstream \text{12 km/h} t \text{12 km/h } (t)
Upstream \text{4 km/h} (1 - t) \text{4 km/h } (1 - t)

The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:

\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \midrule \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.25&& \end{array}

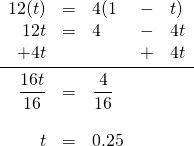
This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling dorsum.

Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h after on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?

Who or What Rate Time Distance
Terry \text{20 km/h} t \text{20 km/h }(t)
Sally \text{80 km/h} (t - \text{6 h}) \text{80 km/h }(t - \text {6 h})

The distance travelled past both is the same. Therefore, the equation to be solved is:

\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \midrule \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}

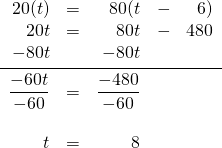
This means that Terry travels for 8 h and Sally only needs 2 h to catch upwardly to him.

On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the auto travel 40 km/h?

Who or What Rate Time Distance
50-five \text{55 km/h} t \text{55 km/h }(t)
Forty \text{40 km/h} (\text{2.5 h}-t) \text{40 km/h }(\text{2.5 h}-t)

The distance travelled by both is 30 km. Therefore, the equation to be solved is:

\begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ &-&100&&&&-100 \\ \midrule &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{array}

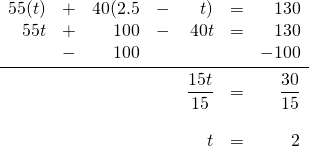
This means that the fourth dimension spent travelling at 40 km/h was 0.5 h.

Distance, time and charge per unit problems take a few variations that mix the unknowns between distance, rate and fourth dimension. They generally involve solving a trouble that uses the combined distance travelled to equal some altitude or a trouble in which the distances travelled by both parties is the same. These distance, rate and fourth dimension issues will exist revisited afterwards in this textbook where quadratic solutions are required to solve them.

Questions

For Questions 1 to 8, observe the equations needed to solve the problems. Exercise not solve.

  1. A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long volition information technology be before the automobiles meet?
  2. Two automobiles are 276 kilometres autonomously and start to travel toward each other at the same time. They travel at rates differing past 5 km/h. If they run into later 6 h, observe the rate of each.
  3. Two trains starting at the aforementioned station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon volition they be 195 kilometres autonomously?
  4. 2 bike messengers, Jerry and Susan, ride in reverse directions. If Jerry rides at the rate of xx km/h, at what rate must Susan ride if they are 150 kilometres autonomously in 5 hours?
  5. A passenger and a freight train outset toward each other at the same time from ii points 300 kilometres autonomously. If the rate of the passenger train exceeds the rate of the freight railroad train by 15 km/h, and they meet after four hours, what must the charge per unit of each be?
  6. Two automobiles started travelling in opposite directions at the aforementioned time from the same point. Their rates were 25 and 35 km/h, respectively. Subsequently how many hours were they 180 kilometres apart?
  7. A human being having ten hours at his disposal made an excursion past bike, riding out at the charge per unit of x km/h and returning on foot at the rate of three km/h. Observe the distance he rode.
  8. A man walks at the rate of 4 km/h. How far can he walk into the state and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?

Solve Questions 9 to 22.

  1. A male child rides away from domicile in an automobile at the rate of 28 km/h and walks back at the charge per unit of iv km/h. The round trip requires 2 hours. How far does he ride?
  2. A motorboat leaves a harbour and travels at an boilerplate speed of fifteen km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of five hours?
  3. A family drove to a resort at an average speed of xxx km/h and afterward returned over the same route at an average speed of 50 km/h. Find the distance to the resort if the total driving time was eight hours.
  4. As part of his flight training, a pupil pilot was required to fly to an aerodrome and and so return. The average speed to the airport was xc km/h, and the average speed returning was 120 km/h. Find the altitude betwixt the 2 airports if the total flying time was vii hours.
  5. Sam starts travelling at iv km/h from a army camp two hours alee of Sue, who travels six km/h in the same direction. How many hours will it take for Sue to take hold of up to Sam?
  6. A human being travels 5 km/h. Later travelling for 6 hours, another man starts at the same place as the first human being did, following at the rate of 8 km/h. When will the 2nd human overtake the kickoff?
  7. A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small-scale island. Two hours afterwards, a cabin cruiser leaves the same harbour and travels at an boilerplate speed of 16 km/h toward the aforementioned isle. How many hours afterward the cabin cruiser leaves will information technology be alongside the motorboat?
  8. A long altitude runner started on a class, running at an boilerplate speed of six km/h. One 60 minutes afterwards, a second runner began the same course at an boilerplate speed of 8 km/h. How long after the 2nd runner started will they overtake the first runner?
  9. Two men are travelling in opposite directions at the rate of xx and 30 km/h at the same time and from the same identify. In how many hours will they be 300 kilometres autonomously?
  10. Two trains showtime at the same time from the same identify and travel in reverse directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres autonomously at the end of iv hours, what is the rate of each?
  11. Two cyclists beginning from the same point and ride in opposite directions. One cyclist rides twice equally fast as the other. In iii hours, they are 72 kilometres autonomously. Find the rate of each cyclist.
  12. 2 minor planes start from the same indicate and fly in opposite directions. The first plane is flying 25 km/h slower than the 2d airplane. In two hours, the planes are 430 kilometres apart. Find the rate of each aeroplane.
  13. On a 130-kilometre trip, a car travelled at an boilerplate speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of ii.5 hours. For how long did the car travel at 40 km/h?
  14. Running at an boilerplate rate of viii m/s, a sprinter ran to the stop of a track and then jogged dorsum to the starting indicate at an average of 3 thousand/s. The sprinter took 55 south to run to the stop of the track and jog dorsum. Detect the length of the track.

<a class="internal" href="/intermediatealgebraberg/dorsum-affair/respond-key-8-viii/">Respond Key 8.8

tatumdoorcall.blogspot.com

Source: https://opentextbc.ca/intermediatealgebraberg/chapter/8-8-rate-word-problems-speed-distance-and-time/

0 Response to "what average speed does he need to reach in his second round"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel